已知直线AB与
轴、
轴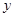分别交于点A和点B，AB=10，且tan∠BAO=
，以OA、OB为边作矩形OACB，点F 在BC上，过点F作AB的垂线，交AB于点D，交OA于点E，若⊙P是△AOB的内切圆，切点分别为M、N、G，
（1）求证：四边形PMON是正方形；
（2）求⊙P的半径;
（3）求当FE与⊙P相交的弦长为2．4时点F的坐标．
相关知识点
推荐套卷
已知直线AB与轴、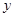轴分别交于点A和点B，AB=10，且tan∠BAO=，以OA、OB为边作矩形OACB，点F 在BC上，过点F作AB的垂线，交AB于点D，交OA于点E，若⊙P是△AOB的内切圆，切点分别为M、N、G，
（1）求证：四边形PMON是正方形；
（2）求⊙P的半径;
（3）求当FE与⊙P相交的弦长为2．4时点F的坐标．
粤公网安备 44130202000953号