如图,把一块含45°直角三角板的锐角顶点与正方形ABCD的顶点A重合.正方形ABCD固定不动,让三角板绕点A旋转.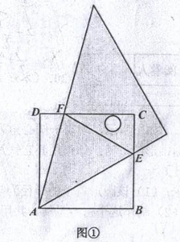
(1)当三角板绕点A旋转到如图①的位置时,含45°角的两边分别与正方形的边BC、DC交于点E、F.求证:EF=BE+DF;
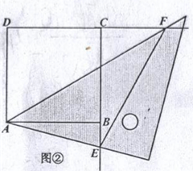
(2)当三角板绕点A旋转到如图②的位置时,含45°角的两边分别与正方形的边CB、DC交于点E、F.试写出EF、BE和DF三条线段满足的数量关系,不必证明;
(3)在图①中,当正方形ABCD的边长为6,EF=5时,BE的长为
(注意:此问占2分)
相关知识点
推荐套卷



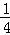 x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;
x2+bx+c与x轴交于A(5,0)、B(﹣1,0)两点,过点A作直线AC⊥x轴,交直线y=2x于点C;

 粤公网安备 44130202000953号
粤公网安备 44130202000953号