如图,在平面直角坐标系中,以点B(0,8)为端点的射线BG∥ 轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与
轴,点A是射线BG上的一个动点(点A与点B不重合).在射线AG上取AD=OB,作线段AD的垂直平分线,垂足为E,且与 轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为
轴交于点F,过点A作AC⊥OA,交射线EF于点C.连接OC、CD,设点A的横坐标为 .
.

(1)用含 的式子表示点E的坐标为 ;
的式子表示点E的坐标为 ;
(2)当点C与点F不重合时,设△OCF的面积为 ,求
,求 与
与 之间的函数关系式.
之间的函数关系式.
(3)当 为何值时,∠OCD=180°?
为何值时,∠OCD=180°?
相关知识点
推荐套卷
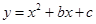 的图象如图所示,其顶点坐标为M(1,-4).
的图象如图所示,其顶点坐标为M(1,-4).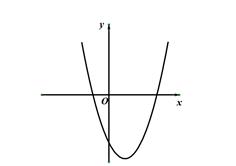
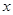 轴下方的部分沿
轴下方的部分沿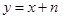 与这个新图象有两个公共点时,求
与这个新图象有两个公共点时,求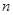 的取值范围.
的取值范围.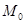 的坐标为(1,0).将线段
的坐标为(1,0).将线段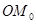 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到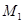 ,使得
,使得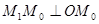 ,得到线段
,得到线段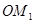 ;又将线段
;又将线段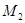 ,使得
,使得 ,得到线段
,得到线段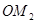 ,如此下去,得到线段
,如此下去,得到线段 ,
,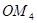 ,…,
,…,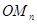 .
.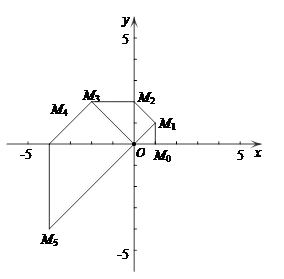
 的周长;
的周长; (
( 0,1,2,3…)的横坐标
0,1,2,3…)的横坐标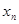 ,纵坐标
,纵坐标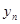 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标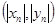 称之为点
称之为点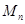 的“绝对坐标”.根据图中点
的“绝对坐标”.根据图中点

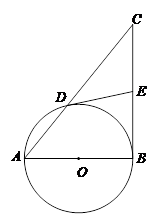
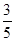 ,BE=
,BE=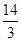 ,求OE的长.
,求OE的长.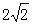 .求四边形
.求四边形 的面积.
的面积.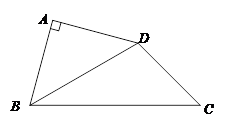
 粤公网安备 44130202000953号
粤公网安备 44130202000953号