如图,正方形ABCD的长为1,点E是AD边上的动点且从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,为DC与EF的交点,请探索: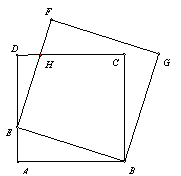
(1)连接CG,线段AE与CG是否相等? 请说明理由.
(2)设AE=x,CG=y,请确定y与x的函数关系式并说明自变量的取值范围.
(3)连接BH,当点E运动到边AD上的某一点时将有△BEH∽△BAE,请你指出这一点的位置,并说明理由.
相关知识点
推荐套卷
如图,正方形ABCD的长为1,点E是AD边上的动点且从点A沿AD向D运动,以BE为边,在BE的上方作正方形BEFG,为DC与EF的交点,请探索:
(1)连接CG,线段AE与CG是否相等? 请说明理由.
(2)设AE=x,CG=y,请确定y与x的函数关系式并说明自变量的取值范围.
(3)连接BH,当点E运动到边AD上的某一点时将有△BEH∽△BAE,请你指出这一点的位置,并说明理由.