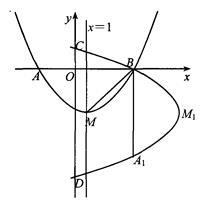
如图，抛物线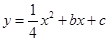
的顶点为M，对称轴是直线x＝1，与x轴的交点为A（－3，0）和B．将抛物线
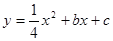绕点B逆时针方向旋转90°，点M1，A1为点M，A旋转后的对应点，旋转后的抛物线与y轴相交于C，D两点．
（1）写出点B的坐标及求抛物线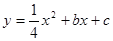的解析式：
（2）求证：∠AMA1=180°
（3）设点P是旋转后抛物线上DM1之间的一动点，是否存在一点P，使四边形PM1MD的面积最大．如果存在，请求出点P的坐标及四边形PM1MD的最大面积；如果不存在，请说明理由．
相关试题
如图．在直角梯形ABCD中，AD//BC，∠B=90°，AG//CD交BC于点G，点E、F分别为AG、CD的中点，连接DE、FG．
（1）求证：四边形DEGF是平行四边形；
（2）如果点G是BC的中点，且BC=12，DC=10，求四边形AGCD的面积．
某中学为丰富学生的校园生活，准备从体育用品商店一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买3个足球和2个篮球共需310元，购买2个足球和5个篮球共需500元。
（1）求购买一个足球、一个篮球各需多少元？
（2）根据学校实际情况，需从体育用品商店一次性购买足球和篮球共96个，要求购买足球和篮球的总费用不超过5720元，这所中学最多可以购买多少个篮球？
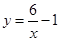与函数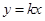
交于点A（2，b）B（-3，m）两点（点A在第一象限），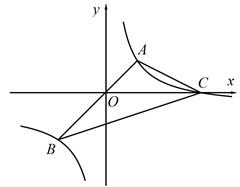
小明在初三复习归纳时发现初中阶段学习了三个非负数，分别是：①
；②
；③
（a是任意实数）．于是他结合所学习的三个非负数的知识，自己编了一道题：已知
，求
的值．请你利用三个非负数的知识解答这个问题．
．相关知识点
推荐套卷
粤公网安备 44130202000953号