下面是小明同学做过的两道题,请先阅读解题过程,然后回答所提出的问题.
(1)计算:(1)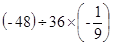 ;
;
解:原式=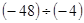 第①步
第①步
=12 第②步
问题:上述解法中,第几步有错?___ ___(填序号即可).
本题的正确解法是:_
(2)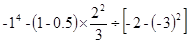 .
.
解:原式=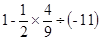 第①步
第①步
=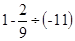 第②步
第②步
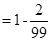 第③步
第③步
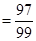 第④步
第④步
问题:上述解法中,第几步有错?___ ___(填序号即可).
本题的正确解法是:
相关知识点
推荐套卷
下面是小明同学做过的两道题,请先阅读解题过程,然后回答所提出的问题.
(1)计算:(1)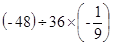 ;
;
解:原式=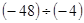 第①步
第①步
=12 第②步
问题:上述解法中,第几步有错?___ ___(填序号即可).
本题的正确解法是:_
(2)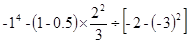 .
.
解:原式=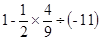 第①步
第①步
=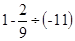 第②步
第②步
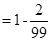 第③步
第③步
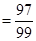 第④步
第④步
问题:上述解法中,第几步有错?___ ___(填序号即可).
本题的正确解法是: