如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径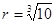 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.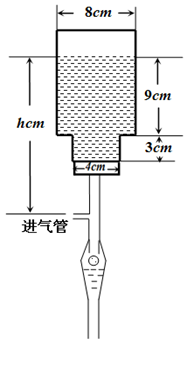
(1)如果瓶内的药液恰好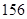 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为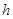 (单位:厘米),已知当
(单位:厘米),已知当 时,
时, .试将
.试将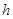 表示为
表示为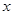 的函数.(注:
的函数.(注: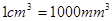 )
)
推荐套卷
如图所示,一种医用输液瓶可以视为两个圆柱的组合体.开始输液时,滴管内匀速滴下球状液体,其中球状液体的半径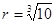 毫米,滴管内液体忽略不计.
毫米,滴管内液体忽略不计.
(1)如果瓶内的药液恰好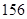 分钟滴完,问每分钟应滴下多少滴?
分钟滴完,问每分钟应滴下多少滴?
(2)在条件(1)下,设输液开始后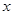 (单位:分钟),瓶内液面与进气管的距离为
(单位:分钟),瓶内液面与进气管的距离为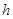 (单位:厘米),已知当
(单位:厘米),已知当 时,
时, .试将
.试将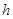 表示为
表示为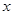 的函数.(注:
的函数.(注: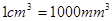 )
)