操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰三角形板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点。图①，②，③是旋转三角板得到的图形中的3种情况。研究：
（1）三角板ABC绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合图②加以证明。
（2）三角板ABC绕点P旋转，△PBE是否能为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由。（图④不用）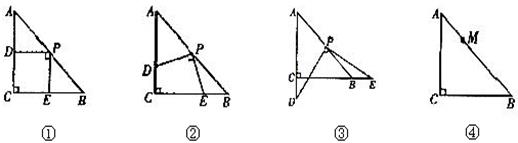
相关试题
在下面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式
+（b-3）2=0，（c-4）2≤0.
（1）求a、b、c的值；
（2）如果在第二象限内有一点P（m，
），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．
、
的坐标分别为(0，1)和(5，
)，
的坐标；
相关知识点
推荐套卷
粤公网安备 44130202000953号