设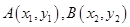
是椭圆
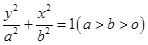上的两点，已知向量
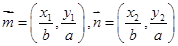，若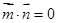
且椭圆的离心率
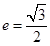，短轴长为2，O为坐标原点．
（Ⅰ） 求椭圆的方程；
（Ⅱ）若直线AB过椭圆的焦点F（0，c），（c为半焦距），求直线AB的斜率k的值；
（Ⅲ）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由．
相关试题
满足
．
上有最小值
，最大值
，求a的取值集合．
集合
,若A="B" ,求
的值．
求
的值;
，求
的值．
；
lg8＋lg5×lg20＋lg22．
、
旁有一矩形花园
，现欲将其扩建成一个更大的三角形花园
，要求点
在射线
在射线
过点
，其中
米，
米．记三角形花园
．
取何值时，推荐套卷
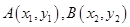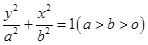设是椭圆上的两点，已知向量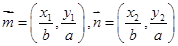，若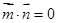且椭圆的离心率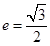，短轴长为2，O为坐标原点．
（Ⅰ） 求椭圆的方程；
（Ⅱ）若直线AB过椭圆的焦点F（0，c），（c为半焦距），求直线AB的斜率k的值；
（Ⅲ）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由．
粤公网安备 44130202000953号