已知椭圆C的方程是
，点A，B分别是椭圆的长轴的左、右端点，左焦点坐标为
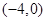，且过点
.
（1）求椭圆C的方程；
（2）已知F是椭圆C的右焦点，以AF为直径的圆记为圆M，试问：过P点能否引圆M的切线，若能，求出这条切线与x轴及圆M的弦PF所对的劣弧围成的图形的面积；若不能，说明理由.
相关试题
≥a+b+c.
（x∈R），
=
·
；如图2，若不在同一平面内的射线OP，OQ和OR上分别存在点P1，P2，点Q1，Q2和点R1，R2，则类似的结论是什么？这个结论正确吗？说明理由.
推荐套卷
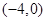已知椭圆C的方程是，点A，B分别是椭圆的长轴的左、右端点，左焦点坐标为，且过点.
（1）求椭圆C的方程；
（2）已知F是椭圆C的右焦点，以AF为直径的圆记为圆M，试问：过P点能否引圆M的切线，若能，求出这条切线与x轴及圆M的弦PF所对的劣弧围成的图形的面积；若不能，说明理由.
粤公网安备 44130202000953号