甲箱子里装有3个白球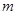 个黑球,乙箱子里装有
个黑球,乙箱子里装有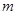 个白球,2个黑球,在一次试验中,分别从这两个箱子里摸出一个球,若它们都是白球,则获奖
个白球,2个黑球,在一次试验中,分别从这两个箱子里摸出一个球,若它们都是白球,则获奖
(1) 当获奖概率最大时,求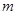 的值;
的值;
(2)在(1)的条件下,班长用上述摸奖方法决定参加游戏的人数,班长有4次摸奖机会(有放回摸取),当班长中奖时已试验次数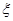 即为参加游戏人数,如4次均未中奖,则
即为参加游戏人数,如4次均未中奖,则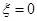 ,求
,求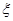 的分布列和
的分布列和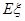 .
.
推荐套卷
甲箱子里装有3个白球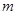 个黑球,乙箱子里装有
个黑球,乙箱子里装有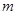 个白球,2个黑球,在一次试验中,分别从这两个箱子里摸出一个球,若它们都是白球,则获奖
个白球,2个黑球,在一次试验中,分别从这两个箱子里摸出一个球,若它们都是白球,则获奖
(1) 当获奖概率最大时,求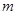 的值;
的值;
(2)在(1)的条件下,班长用上述摸奖方法决定参加游戏的人数,班长有4次摸奖机会(有放回摸取),当班长中奖时已试验次数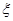 即为参加游戏人数,如4次均未中奖,则
即为参加游戏人数,如4次均未中奖,则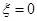 ,求
,求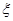 的分布列和
的分布列和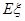 .
.