高一某班共有学生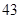 人,据统计原来每人每年用于购买饮料的平均支出是
人,据统计原来每人每年用于购买饮料的平均支出是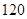 元。若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用
元。若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用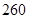 元,其中,纯净水的销售价
元,其中,纯净水的销售价 (元
(元 桶)与年购买总量
桶)与年购买总量 (桶)之间满足如图直线所示关系.
(桶)之间满足如图直线所示关系.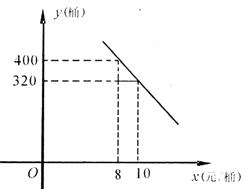
(1)求 关于
关于 的函数关系式,并写出函数的定义域;
的函数关系式,并写出函数的定义域;
(2)若该班每年需要纯净水 桶,请你根据提供的信息比较,该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用,哪一个更少?说明你的理由.
桶,请你根据提供的信息比较,该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用,哪一个更少?说明你的理由.
推荐套卷
高一某班共有学生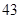 人,据统计原来每人每年用于购买饮料的平均支出是
人,据统计原来每人每年用于购买饮料的平均支出是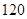 元。若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用
元。若该班全体学生改饮某品牌的桶装纯净水,经测算和市场调查,其年总费用由两部分组成,一部分是购买纯净水的费用,另一部分是其它费用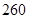 元,其中,纯净水的销售价
元,其中,纯净水的销售价 (元
(元 桶)与年购买总量
桶)与年购买总量 (桶)之间满足如图直线所示关系.
(桶)之间满足如图直线所示关系.
(1)求 关于
关于 的函数关系式,并写出函数的定义域;
的函数关系式,并写出函数的定义域;
(2)若该班每年需要纯净水 桶,请你根据提供的信息比较,该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用,哪一个更少?说明你的理由.
桶,请你根据提供的信息比较,该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用,哪一个更少?说明你的理由.