某市努力改造空气质量,近年来空气质量明显好转,根据市环境保护局公布的2006—2010这五年各年的全年空气质量优良的天数,绘制折线图如图所示,根据图中的信息回答:
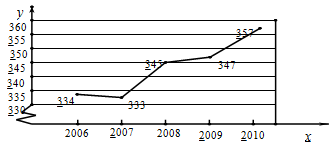
(1)这五年的全年空气质量优良天数的中位数是 ,极差是 ;
(2)这五年的全年空气质量优良天数与它前一年相比较,增加最多的是 年,(填写年份)
(3)求这五年的全年空气质量优良天数的平均数。
相关知识点
推荐套卷
某市努力改造空气质量,近年来空气质量明显好转,根据市环境保护局公布的2006—2010这五年各年的全年空气质量优良的天数,绘制折线图如图所示,根据图中的信息回答:

(1)这五年的全年空气质量优良天数的中位数是 ,极差是 ;
(2)这五年的全年空气质量优良天数与它前一年相比较,增加最多的是 年,(填写年份)
(3)求这五年的全年空气质量优良天数的平均数。