某商场销售一种西装和领带,西装每套定价500元,领带每条定价60元.“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.方案一:买一套西装送一条领带;方案二:西装和领带都按定价的90%付款.现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款______________元.(用含x的代数式表示)若该客户按方案二购买,需付款_____________元.(用含x的代数式表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
相关知识点
推荐套卷
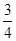 ﹣(﹣
﹣(﹣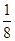 )+3
)+3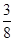 +(﹣2
+(﹣2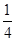 )
)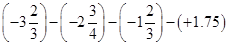 .
.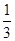 ﹣(3
﹣(3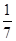 )﹣4
)﹣4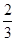 ﹣(﹣8
﹣(﹣8 粤公网安备 44130202000953号
粤公网安备 44130202000953号