某初级中学共有学生2 000名,各年级男、女生人数如下表:
| |
初一年级 |
初二年级 |
初三年级 |
| 女生 |
373 |
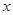 |
 |
| 男生 |
377 |
370 |
 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求x的值.
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知y≥245,z≥245,求初三年级中女生比男生多的概率.
推荐套卷
某初级中学共有学生2 000名,各年级男、女生人数如下表:
| |
初一年级 |
初二年级 |
初三年级 |
| 女生 |
373 |
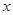 |
 |
| 男生 |
377 |
370 |
 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求x的值.
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知y≥245,z≥245,求初三年级中女生比男生多的概率.