已知三点O(0,0)，A(－2,1)，B(2,1)，曲线C上任意一点M(x，y)满足|
＋
|＝
·(
＋
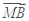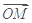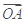)＋2.
(1)求曲线C的方程；
(2)点Q(x0，y0)(－2<x0<2)是曲线C上的动点，曲线C在点Q处的切线为
，点P的坐标是(0，－1)，与PA，PB分别交于点D，E，求△QAB与△PDE的面积之比．
相关试题
满足
，且
。
上，
的图象恒在
的图象上方，试确定实数
的范围。
，
的奇偶性；
上是减函数。
求函数
的最大值和最小值。
上的函数
是偶函数，且
时，
，
时，求
解析式；推荐套卷
已知三点O(0,0)，A(－2,1)，B(2,1)，曲线C上任意一点M(x，y)满足|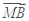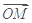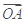＋|＝·(＋)＋2.
(1)求曲线C的方程；
(2)点Q(x0，y0)(－2<x0<2)是曲线C上的动点，曲线C在点Q处的切线为，点P的坐标是(0，－1)，与PA，PB分别交于点D，E，求△QAB与△PDE的面积之比．
粤公网安备 44130202000953号