（本小题满分14分）
设双曲线C：
（a>0，b>0）的一个焦点坐标为（
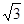，0），离心率
， A、B是双曲线上的两点，AB的中点M（1，2）．
（1）求双曲线C的方程；
（2）求直线AB方程；
（3）如果线段AB的垂直平分线与双曲线交于C、D两点，那么A、B、C、D四点是否共圆？为什么？
沿
轴向左平移３个单位，再沿
轴向上平移１个单位后，回到原来的位置，试求直线
中，顶点
，
，
的平分线的方程是
．求顶点
的坐标．
的坐标是
，底边一个端点
的坐标是
，求另一个端点
的轨迹方程，并说明它是什么图形．
，
距离相等的点的坐标
满足的条件．相关知识点
推荐套卷
（本小题满分14分）
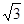设双曲线C：（a>0，b>0）的一个焦点坐标为（，0），离心率， A、B是双曲线上的两点，AB的中点M（1，2）．
（1）求双曲线C的方程；
（2）求直线AB方程；
（3）如果线段AB的垂直平分线与双曲线交于C、D两点，那么A、B、C、D四点是否共圆？为什么？
粤公网安备 44130202000953号