(1)如图1,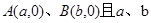 满足
满足 .
.
①求 的值;
的值;
②若C(-6,0),连CB,作BE⊥CB,垂足为B,且BC=BE,连AE交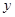 轴于P,求P点坐标.
轴于P,求P点坐标.
(2)如图2,若A(6,0),B(0,3),点Q从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点Q运动时间为 秒,过Q点作直线AB的垂线,垂足为D,直线QD与
秒,过Q点作直线AB的垂线,垂足为D,直线QD与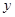 轴交于E点,在点Q的运动过程中,一定存在△EOQ≌△AOB,请直接写出存在的
轴交于E点,在点Q的运动过程中,一定存在△EOQ≌△AOB,请直接写出存在的 值以及相应的E点坐标.
值以及相应的E点坐标.
相关知识点
推荐套卷
(1)如图1,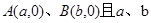 满足
满足 .
.
①求 的值;
的值;
②若C(-6,0),连CB,作BE⊥CB,垂足为B,且BC=BE,连AE交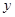 轴于P,求P点坐标.
轴于P,求P点坐标.
(2)如图2,若A(6,0),B(0,3),点Q从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点Q运动时间为 秒,过Q点作直线AB的垂线,垂足为D,直线QD与
秒,过Q点作直线AB的垂线,垂足为D,直线QD与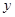 轴交于E点,在点Q的运动过程中,一定存在△EOQ≌△AOB,请直接写出存在的
轴交于E点,在点Q的运动过程中,一定存在△EOQ≌△AOB,请直接写出存在的 值以及相应的E点坐标.
值以及相应的E点坐标.