如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在函数y=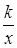
（k>0,x>0）的图象上，点D的坐标为（4，3）．
（1）求k的值；
（2）若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y=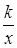（k>0,x>0）的图象上时，求菱形ABCD沿x轴正方向平移的距离．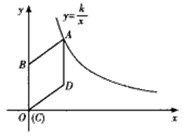
如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在函数y=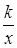（k>0,x>0）的图象上，点D的坐标为（4，3）．
（1）求k的值；
（2）若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y=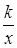（k>0,x>0）的图象上时，求菱形ABCD沿x轴正方向平移的距离．
．
粤公网安备 44130202000953号