（玉林防城港）已知：一次函数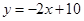
的图象与反比例函数
（
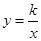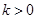）的图象相交于A，B两点（A在B的右侧）．
（1）当A（4，2）时，求反比例函数的解析式及B点的坐标；
（2）在（1）的条件下，反比例函数图象的另一支上是否存在一点P，使△PAB是以AB为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
（3）当A（a，﹣2a+10），B（b，﹣2b+10）时，直线OA与此反比例函数图象的另一支交于另一点C，连接BC交y轴于点D．若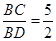
，求△ABC的面积．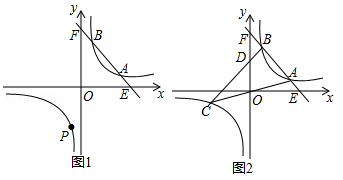
（玉林防城港）已知：一次函数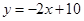的图象与反比例函数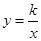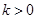（）的图象相交于A，B两点（A在B的右侧）．
（1）当A（4，2）时，求反比例函数的解析式及B点的坐标；
（2）在（1）的条件下，反比例函数图象的另一支上是否存在一点P，使△PAB是以AB为直角边的直角三角形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．
（3）当A（a，﹣2a+10），B（b，﹣2b+10）时，直线OA与此反比例函数图象的另一支交于另一点C，连接BC交y轴于点D．若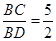，求△ABC的面积．
的值．
粤公网安备 44130202000953号