在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△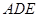 绕点A逆时针旋转,得到等腰Rt△
绕点A逆时针旋转,得到等腰Rt△ ,设旋转角为
,设旋转角为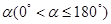 ,记直线
,记直线 与
与 的交点为P.
的交点为P.
(1)如图1,当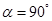 时,线段
时,线段 的长等于 ,线段
的长等于 ,线段 的长等于 ;(直接填写结果)
的长等于 ;(直接填写结果)
(2)如图2,当 时,求证:
时,求证: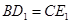 ,且
,且 ;
;
(3)①设BC的中点为M,则线段PM的长为 ;②点P到AB所在直线的距离的最大值为 .(直接填写结果)


在Rt△ABC中,∠A=90°,AC=AB=4, D,E分别是AB,AC的中点.若等腰Rt△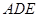 绕点A逆时针旋转,得到等腰Rt△
绕点A逆时针旋转,得到等腰Rt△ ,设旋转角为
,设旋转角为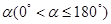 ,记直线
,记直线 与
与 的交点为P.
的交点为P.
(1)如图1,当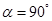 时,线段
时,线段 的长等于 ,线段
的长等于 ,线段 的长等于 ;(直接填写结果)
的长等于 ;(直接填写结果)
(2)如图2,当 时,求证:
时,求证: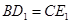 ,且
,且 ;
;
(3)①设BC的中点为M,则线段PM的长为 ;②点P到AB所在直线的距离的最大值为 .(直接填写结果)

