如图，在▱ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD．连接BE、BF，使它们分别与AO相交于点G、H．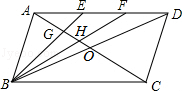
（1）求EG：BG的值；
（2）求证：AG=OG；
（3）设AG=a，GH=b，HO=c，求a：b：c的值．
相关试题
如图，在▱ABCD中，对角线AC、BD相交于点O，点E、F是AD上的点，且AE=EF=FD．连接BE、BF，使它们分别与AO相交于点G、H．
（1）求EG：BG的值；
（2）求证：AG=OG；
（3）设AG=a，GH=b，HO=c，求a：b：c的值．
粤公网安备 44130202000953号