(·湖北鄂州,21题,9分)如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量 ,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).
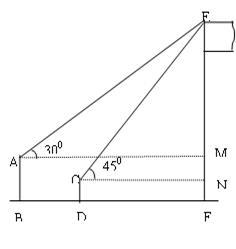
(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数. 参考数据:
参考数据: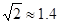 ,
,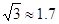 )
)
(·湖北鄂州,21题,9分)如图,某数学兴趣小组在活动课上测量学校旗杆的高度.已知小亮站着测量 ,眼睛与地面的距离(AB)是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离(CD)是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).

(1)求小敏到旗杆的距离DF.(结果保留根号)
(2)求旗杆EF的高度.(结果保留整数. 参考数据:
参考数据: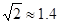 ,
,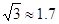 )
)