(·湖南株洲)已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q,
(1)当点P,运动到Q、C两点重合时(如图1),求AP的长。
(2)点运动过程中,有几个位置(几种情况)使△CQD的面积为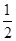 ?( 直接写出答案)
?( 直接写出答案)
(3)当使△CQD的面积为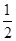 ,且Q位于以CD为直径的的上半圆上,CQ>QD时(如图2),求AP的长。
,且Q位于以CD为直径的的上半圆上,CQ>QD时(如图2),求AP的长。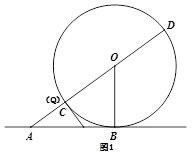
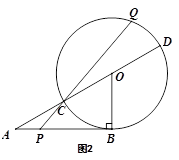
(·湖南株洲)已知AB是圆O的切线,切点为B,直线AO交圆O于C、D两点,CD=2,∠DAB=30°,动点P在直线AB上运动,PC交圆O于另一点Q,
(1)当点P,运动到Q、C两点重合时(如图1),求AP的长。
(2)点运动过程中,有几个位置(几种情况)使△CQD的面积为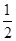 ?( 直接写出答案)
?( 直接写出答案)
(3)当使△CQD的面积为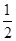 ,且Q位于以CD为直径的的上半圆上,CQ>QD时(如图2),求AP的长。
,且Q位于以CD为直径的的上半圆上,CQ>QD时(如图2),求AP的长。
