(·湖北衡阳,27题,分)(本小题满分10分)如图,顶点M在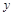 轴上的抛物线与直线
轴上的抛物线与直线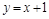 相交于A、B两点,且点A在
相交于A、B两点,且点A在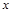 轴上,点B的横坐标为2,连结AM、BM.
轴上,点B的横坐标为2,连结AM、BM.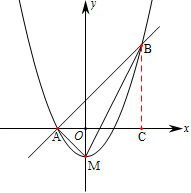
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线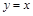 的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(
的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(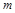 ,
,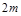 ),当
),当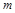 满足什么条件时,平移后的抛物线总有不动点?
满足什么条件时,平移后的抛物线总有不动点?
(·湖北衡阳,27题,分)(本小题满分10分)如图,顶点M在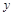 轴上的抛物线与直线
轴上的抛物线与直线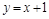 相交于A、B两点,且点A在
相交于A、B两点,且点A在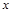 轴上,点B的横坐标为2,连结AM、BM.
轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线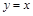 的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(
的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(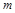 ,
,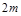 ),当
),当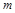 满足什么条件时,平移后的抛物线总有不动点?
满足什么条件时,平移后的抛物线总有不动点?