(眉山)(本小题满分9分)如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.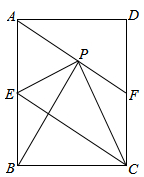
(眉山)(本小题满分9分)如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)若△AEP是等边三角形,连结BP,求证:△APB≌△EPC;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.