(资阳)如图,直线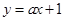 与x轴、y轴分别相交于A、B两点,与双曲线
与x轴、y轴分别相交于A、B两点,与双曲线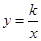 (
( )相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.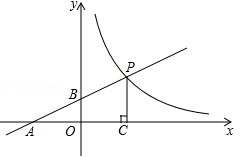
(资阳)如图,直线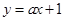 与x轴、y轴分别相交于A、B两点,与双曲线
与x轴、y轴分别相交于A、B两点,与双曲线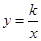 (
( )相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.