(宜宾)如图,抛物线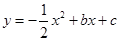 与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
(1)求抛物线的解析式;
(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.
①当四边形OMHN为矩形时,求点H的坐标;
②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.
(宜宾)如图,抛物线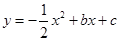 与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
(1)求抛物线的解析式;
(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.
①当四边形OMHN为矩形时,求点H的坐标;
②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.