(乐山)如图1,二次函数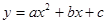 的图象与
的图象与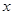 轴分别交于A、B两点,与
轴分别交于A、B两点,与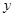 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程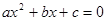 的两根为-8、2.
的两根为-8、2.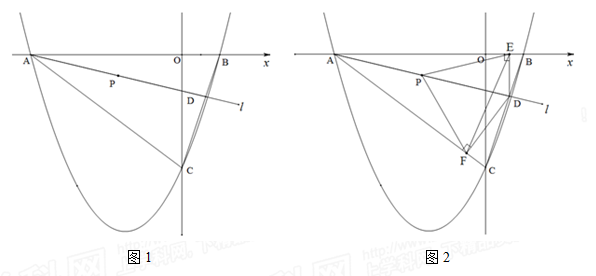
(1)求二次函数的解析式;
(2)直线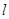 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止,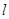 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直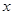 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在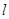 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结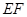 ,求△PEF周长的最小值.
,求△PEF周长的最小值.
(乐山)如图1,二次函数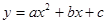 的图象与
的图象与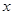 轴分别交于A、B两点,与
轴分别交于A、B两点,与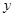 轴交于点C.若tan∠ABC=3,一元二次方程
轴交于点C.若tan∠ABC=3,一元二次方程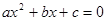 的两根为-8、2.
的两根为-8、2.
(1)求二次函数的解析式;
(2)直线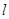 绕点A以AB为起始位置顺时针旋转到AC位置停止,
绕点A以AB为起始位置顺时针旋转到AC位置停止,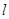 与线段BC交于点D,P是AD的中点.
与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直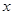 轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在
轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在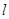 运动过程中,∠EPF的大小是否改变?请说明理由;
运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结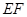 ,求△PEF周长的最小值.
,求△PEF周长的最小值.