（资阳）学校需要购买一批篮球和足球，已知一个篮球比一个足球的进价高30元，买两个篮球和三个足球一共需要510元．
（1）求篮球和足球的单价；
（2）根据实际需要，学校决定购买篮球和足球共100个，其中篮球购买的数量不少于足球数量的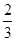
，学校可用于购买这批篮球和足球的资金最多为10500元．请问有几种购买方案？
（3）若购买篮球x个，学校购买这批篮球和足球的总费用为y（元），在（2）的条件下，求哪种方案能使y最小，并求出y的最小值．
相关试题
（资阳）学校需要购买一批篮球和足球，已知一个篮球比一个足球的进价高30元，买两个篮球和三个足球一共需要510元．
（1）求篮球和足球的单价；
（2）根据实际需要，学校决定购买篮球和足球共100个，其中篮球购买的数量不少于足球数量的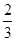，学校可用于购买这批篮球和足球的资金最多为10500元．请问有几种购买方案？
（3）若购买篮球x个，学校购买这批篮球和足球的总费用为y（元），在（2）的条件下，求哪种方案能使y最小，并求出y的最小值．
中，对角线AC与BD交于点O，△ABO≌△CDO.
，其中x=
.
并把解集在数轴上表示出来.
中，点A(2,m)，B(-3,n)为两动点，其中m﹥1，连结
，
，作
轴于
点，
轴于
点．
时，抛物线经过
两点且以
轴为对称轴，求抛物线对应的二次函数的关系式
交
，过点
交抛物线于
两点，问是否存在直线
粤公网安备 44130202000953号