已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣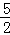 ).
).
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.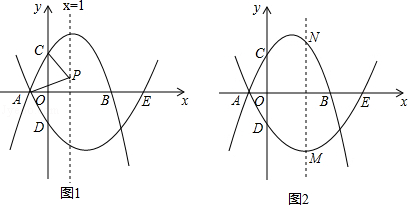
已知:抛物线l1:y=﹣x2+bx+3交x轴于点A,B,(点A在点B的左侧),交y轴于点C,其对称轴为x=1,抛物线l2经过点A,与x轴的另一个交点为E(5,0),交y轴于点D(0,﹣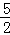 ).
).
(1)求抛物线l2的函数表达式;
(2)P为直线x=1上一动点,连接PA,PC,当PA=PC时,求点P的坐标;
(3)M为抛物线l2上一动点,过点M作直线MN∥y轴,交抛物线l1于点N,求点M自点A运动至点E的过程中,线段MN长度的最大值.