如图，在平面直角坐标系中，△ABC的顶点A在x轴负半轴上，顶点C在x轴正半轴上，顶点B在第一象限，过点B作BD⊥y轴于点D，线段OA，OC的长是一元二次方程x2﹣12x+36=0的两根，BC=4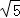
，∠BAC=45°．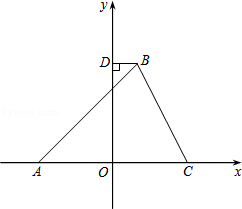
（1）求点A，C的坐标；
（2）反比例函数y=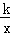
的图象经过点B，求k的值；
（3）在y轴上是否存在点P，使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似？若存在，请写出满足条件的点P的个数，并直接写出其中两个点P的坐标；若不存在，请说明理由．
相关试题
如图，在平面直角坐标系中，△ABC的顶点A在x轴负半轴上，顶点C在x轴正半轴上，顶点B在第一象限，过点B作BD⊥y轴于点D，线段OA，OC的长是一元二次方程x2﹣12x+36=0的两根，BC=4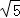，∠BAC=45°．
（1）求点A，C的坐标；
（2）反比例函数y=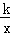的图象经过点B，求k的值；
（3）在y轴上是否存在点P，使以P，B，D为顶点的三角形与以P，O，A为顶点的三角形相似？若存在，请写出满足条件的点P的个数，并直接写出其中两个点P的坐标；若不存在，请说明理由．
，其中
.
.
.
，设运动时间为t（t>0）秒．
粤公网安备 44130202000953号