（·黑龙江绥化）如图，已知抛物线y=ax2+bx+c与x轴交于点A、B，与直线AC:y=－x－6交y轴于点C、D，点D是抛物线的顶点，且横坐标为－2．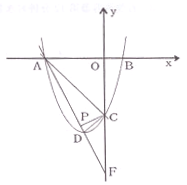
（1）求出抛物线的解析式。
（2）判断△ACD的形状，并说明理由。
（3）直线AD交y轴于点F，在线段AD上是否存在一点P，使∠ADC=∠PCF ．若存在，直接写出点P的坐标；若不存在，说明理由。
相关试题
（·黑龙江绥化）如图，已知抛物线y=ax2+bx+c与x轴交于点A、B，与直线AC:y=－x－6交y轴于点C、D，点D是抛物线的顶点，且横坐标为－2．
（1）求出抛物线的解析式。
（2）判断△ACD的形状，并说明理由。
（3）直线AD交y轴于点F，在线段AD上是否存在一点P，使∠ADC=∠PCF ．若存在，直接写出点P的坐标；若不存在，说明理由。
中，
∥
，
，
⊥
，延长
至点
，使
．
的度数．
为等腰三角形．
中，
是
边上一点，
的延长线交
的延长线于点
，
⊥
，垂足为
，且
．
；
，BD⊥AD，求BC，CD及OB的长.
（
粤公网安备 44130202000953号