邮递员骑车从邮局出发,先向南骑行3 km到达A村,继续向南骑行2 km到达B村,然后向北骑行8km到达C村,最后回到邮局.以邮局为原点,以向南方向为正方向,用l cm表示1 km,画出数轴如图.
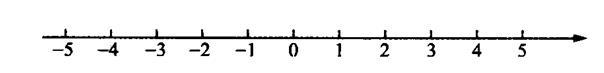
(1)在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有 km;
(3)邮递员一共骑行了 km.
相关知识点
推荐套卷
邮递员骑车从邮局出发,先向南骑行3 km到达A村,继续向南骑行2 km到达B村,然后向北骑行8km到达C村,最后回到邮局.以邮局为原点,以向南方向为正方向,用l cm表示1 km,画出数轴如图.
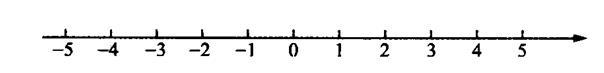
(1)在该数轴上表示出A、B、C三个村庄的位置;
(2)C村离A村有 km;
(3)邮递员一共骑行了 km.