（本题10分））如图，半径为1个单位的圆片上有一点Q与数轴上的原点重合（提示：圆的周长C=2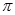
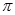r， 保留）．
（1）把圆片沿数轴滚动1周，点Q到达数轴上点A的位置，点A表示的数是___；
（2）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：+2， -1， -5， +4， +3， -2．
①第几次滚动后，Q点距离原点最近？第几次滚动后，Q点距离原点最远？
②当圆片结束运动时，Q点运动的路程共有多少?此时点Q所表示的数是多少?
如图，在平面直角坐标系中，直线l与x轴相交于点M，与y轴相交于点N，Rt△MON的外心为点A（
，-2），反比例函数y=
（x＞0）的图象过点A．
（1）求直线l的解析式；
（2）在函数y=（x＞0）的图象上取异于点A的一点B，作BC⊥x轴于点C，连接OB交直线l于点P．若△ONP的面积是△OBC面积的3倍，求点P的坐标．
如图，在一笔直的海岸线l上有A、B两个观测站，A在B的正东方向，BP=3
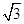（单位：km）有一艘小船在点P处，从A测得小船在北偏西60°的方向，从B测得小船在北偏东45°的方向．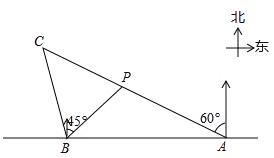
（1）求A、B两个观测站之间的距离；
（2）小船从点P处沿射线AP的方向以千米/时的速度进行沿途考查，航行一段时间后到达点C处，此时，从B测得小船在北偏西15°的方向，求小船沿途考察的时间．（结果有根号的保留根号）
某大学举办教工男子篮球赛，由大学各个院系教工组成A、B、C、D、E五个代表队，由大学附属单位组成F、G、H三个代表队．通过抽签分组，比赛共分上下两个半区，上半区有A、D、E、G四个代表队，下半区有B、C、F、H四个代表队．若从上下半区各随机抽取一个代表队进行首场比赛，请列表或画树状图写出所有可能的结果，并计算首场比赛的两个代表队都是大学附属单位代表队的概率．
粤公网安备 44130202000953号