)阅读下面的材料,回答问题:
爱动脑筋的小明在学过用配方法解一元二次方程后,他发现二次三项式也可以配方,从而解决一些问题。例如: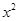 -6x+10=(
-6x+10=(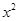 -6x+9-9)+10=
-6x+9-9)+10=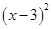 -9+10=
-9+10=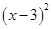 +1≥1;因此
+1≥1;因此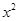 -6x+10有最小值是1;
-6x+10有最小值是1;
(1)尝试:-3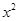 -6x+5=-3(
-6x+5=-3(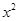 +2x+1-1)+5=-3
+2x+1-1)+5=-3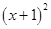 +8,因此-3
+8,因此-3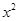 -6x+5有最大值是______
-6x+5有最大值是______
(2)应用:有长为24米的篱笆,一面利用墙(墙的最大可用长度为a为15米),围成一个的长方形花圃。能围成面积最大的花圃吗?如果能,请求出最大面积.
相关知识点
推荐套卷
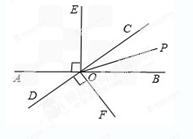
 ∠= 度.
∠= 度.
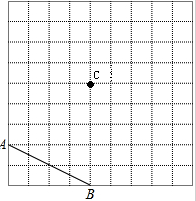
 当
当 时,求
时,求 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号