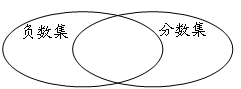
（1）如图，两个圈分别表示负数集和分数集，请将﹣50%，2012，0.618，﹣3，
，0，5.9，﹣3.14，﹣92中，符合要求的数填入相应的圈中；
（2）在数轴上表示下列四个数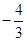
，
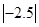，0，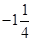
，并把它们用“＜”号连接起来．
（1）
（2）
（1）如图，两个圈分别表示负数集和分数集，请将﹣50%，2012，0.618，﹣3，，0，5.9，﹣3.14，﹣92中，符合要求的数填入相应的圈中；
（2）在数轴上表示下列四个数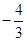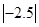，，0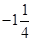，，并把它们用“＜”号连接起来．
（1） （2）
粤公网安备 44130202000953号