已知:如图,在▱ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.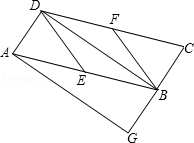
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
相关知识点
推荐套卷
已知:如图,在▱ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△ADE≌△CBF;
(2)若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.