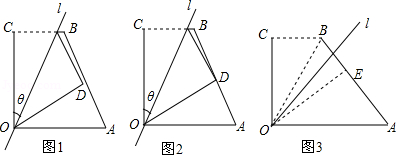
如图1，四边形OABC中，OA=a，OC=3，BC=2，∠AOC=∠BCO=90°，经过点O的直线l将四边形分成两部分，直线l与
OC所成的角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处（如图1）．
（1）若折叠后点D恰为AB的中点（如图2），则θ= ；
（2）若θ=45°，四边形OABC的直角∠OCB沿直线l折叠后，点B落在点四边形OABC的边AB上的E处（如图3），求a的值．
相关试题
2011年4月21日是重庆一中80周年校庆日，学校准备进一步美化校园，在校内一块四边形草坪内栽上一棵银杏树如图，要求银杏树的位置点P到边AB、BC的距离相等，并且P到点A、D的距离也相等．请用尺规作图作出银杏树的位置点P（不写作法，保留作图痕迹）．
相关知识点
推荐套卷
粤公网安备 44130202000953号