已知二次函数
为常数，且
）满足条件：
，且方程
有两个相等的实数根．
（1）求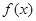
的解析式；
（2）求函数在区间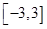
上的最大值和最小值；
（3）是否存在实数
使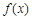
的定义域和值域分别为
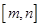和
，如果存在，求出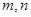
的值，如不存在，请说明理由．
为数列
的前
项和，
，
，
.
，求数列
的通项公式；
，求
的取值范围．
为数列
的前
项和，已知
时，
是等比数列；
的通项公式
的首项
，
，
…．证明：数列
是等比数列；
和
满足：
，
，
，其中
为实数，
.
为等比数列
前
项和，
，
，
，前
.相关知识点
推荐套卷
已知二次函数 为常数，且）满足条件：，且方程有两个相等的实数根．
（1）求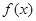的解析式；
（2）求函数在区间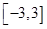上的最大值和最小值；
（3）是否存在实数使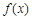的定义域和值域分别为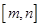和，如果存在，求出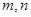的值，如不存在，请说明理由．
粤公网安备 44130202000953号