如图,在直角坐标系中,Rt△OAB的直角顶点A在x轴上,OA=4,AB=3.动点M从点A出发,以每秒1个单位长度的速度,沿AO向终点O移动;同时点N从点O出发,以每秒1.25个单位长度的速度,沿OB向终点B移动.当两个动点运动了x秒(0<x<4)时,解答下列问题:
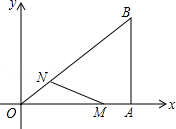
(1)求点N的坐标(用含x的代数式表示);
(2)设△OMN的面积是S,求S与x之间的函数表达式;当x为何值时,S有最大值?最大值是多少?
(3)在两个动点运动过程中,是否存在某一时刻,使△OMN是直角三角形?若存在,求出x的值;若不存在,请说明理由.