如图,已知一条直线过点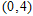 ,且与抛物线
,且与抛物线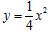 交于A,B两点,其中点A的横坐标是
交于A,B两点,其中点A的横坐标是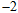 .
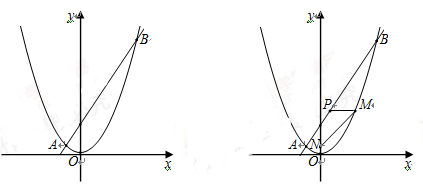
.
(1)求这条直线的函数关系式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标;若不存在,请说明理由;
(3) 过线段AB上一点P,作PM //x轴,交抛物线于点M,点M在第一象限,点N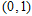 ,当点M的横坐标为何值时,
,当点M的横坐标为何值时,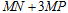 的长度最大?最大值是多少?
的长度最大?最大值是多少?
如图,已知一条直线过点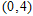 ,且与抛物线
,且与抛物线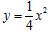 交于A,B两点,其中点A的横坐标是
交于A,B两点,其中点A的横坐标是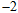 .
.
(1)求这条直线的函数关系式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标;若不存在,请说明理由;
(3) 过线段AB上一点P,作PM //x轴,交抛物线于点M,点M在第一象限,点N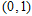 ,当点M的横坐标为何值时,
,当点M的横坐标为何值时,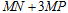 的长度最大?最大值是多少?
的长度最大?最大值是多少?