在平面直角坐标系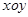 中,椭圆
中,椭圆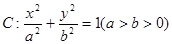 的焦距为2,一个顶点与两个焦点组成一个等边三角形.
的焦距为2,一个顶点与两个焦点组成一个等边三角形.
(Ⅰ)求椭圆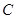 的标准方程;
的标准方程;
(Ⅱ)椭圆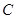 的右焦点为
的右焦点为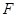 ,过
,过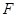 点的两条互相垂直的直线
点的两条互相垂直的直线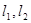 ,直线
,直线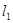 与椭圆
与椭圆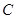 交于
交于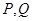 两点,直线
两点,直线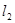 与直线
与直线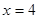 交于
交于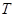 点.
点.
(i)求证:线段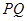 的中点
的中点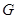 在直线
在直线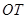 上;
上;
(ii)求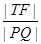 的取值范围.
的取值范围.
推荐套卷
在平面直角坐标系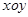 中,椭圆
中,椭圆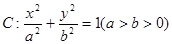 的焦距为2,一个顶点与两个焦点组成一个等边三角形.
的焦距为2,一个顶点与两个焦点组成一个等边三角形.
(Ⅰ)求椭圆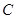 的标准方程;
的标准方程;
(Ⅱ)椭圆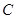 的右焦点为
的右焦点为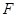 ,过
,过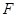 点的两条互相垂直的直线
点的两条互相垂直的直线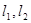 ,直线
,直线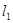 与椭圆
与椭圆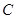 交于
交于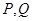 两点,直线
两点,直线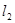 与直线
与直线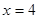 交于
交于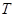 点.
点.
(i)求证:线段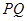 的中点
的中点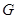 在直线
在直线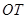 上;
上;
(ii)求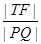 的取值范围.
的取值范围.