如图,某广场为一半径为80米的半圆形区域,现准备在其一扇形区域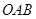 内建两个圆形花坛,该扇形的圆心角为变量
内建两个圆形花坛,该扇形的圆心角为变量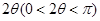 ,其中半径较大的花坛
,其中半径较大的花坛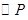 内切于扇形,半径较小的花坛
内切于扇形,半径较小的花坛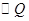 与
与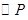 外切,且与
外切,且与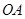 、
、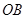 相切.
相切.
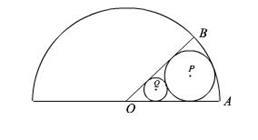
(1)求半径较大的花坛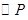 的半径(用
的半径(用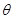 表示);
表示);
(2)求半径较小的花坛的半径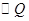 的最大值.
的最大值.
推荐套卷
如图,某广场为一半径为80米的半圆形区域,现准备在其一扇形区域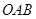 内建两个圆形花坛,该扇形的圆心角为变量
内建两个圆形花坛,该扇形的圆心角为变量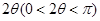 ,其中半径较大的花坛
,其中半径较大的花坛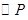 内切于扇形,半径较小的花坛
内切于扇形,半径较小的花坛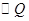 与
与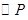 外切,且与
外切,且与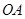 、
、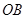 相切.
相切.

(1)求半径较大的花坛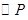 的半径(用
的半径(用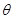 表示);
表示);
(2)求半径较小的花坛的半径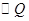 的最大值.
的最大值.