甲、乙两人玩转盘游戏，该游戏规则是这样的：一个质地均匀的标有12等分数字格的转盘（如图），甲、乙两人各转转盘一次，转盘停止时指针所指的数字为该人的得分．（假设指针不能指向分界线）现甲先转，乙后转，求下列事件发生的概率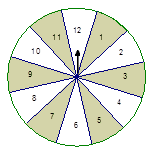
（1）甲得分超过7分的概率．
（2）甲得7分，且乙得10分的概率
（3）甲得5分且获胜的概率．
，（
为常数）．
的最小正周期；
上最大值与最小值之和为3，求
的值；
是第一象限角，试确定
的象限．
，求
的值．
,计算：
；（2）
.
．
的终边经过点P
,求角
推荐套卷
甲、乙两人玩转盘游戏，该游戏规则是这样的：一个质地均匀的标有12等分数字格的转盘（如图），甲、乙两人各转转盘一次，转盘停止时指针所指的数字为该人的得分．（假设指针不能指向分界线）现甲先转，乙后转，求下列事件发生的概率
（1）甲得分超过7分的概率．
（2）甲得7分，且乙得10分的概率
（3）甲得5分且获胜的概率．
粤公网安备 44130202000953号