（本小题满分6分）如图，在平面直角坐标系中，点O是坐标原点，Rt△OAB的直角顶点B在y轴的正半轴上，以原点O为位似中心，位似比为2:1，把△OAB放大，放大后的三角形为△OCD，把△OAB绕点O逆时针旋转90º后得△OEF，点A的坐标是（1，t）．
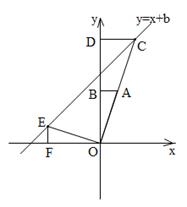
（1）分别写出点C、E的坐标C（ ， ），E（ ， ）（用含t的代数式表示）；
（2）如果直线y＝x＋b经过E、C两点，试求出t与b的值．
，并从0，-1, 2中选一个合适的数作为
的值带入求值．
，求线段AB的长。
相关知识点
推荐套卷
（本小题满分6分）如图，在平面直角坐标系中，点O是坐标原点，Rt△OAB的直角顶点B在y轴的正半轴上，以原点O为位似中心，位似比为2:1，把△OAB放大，放大后的三角形为△OCD，把△OAB绕点O逆时针旋转90º后得△OEF，点A的坐标是（1，t）．
（1）分别写出点C、E的坐标C（ ， ），E（ ， ）（用含t的代数式表示）；
（2）如果直线y＝x＋b经过E、C两点，试求出t与b的值．
粤公网安备 44130202000953号