（本小题满分12分）抛物线
的焦点为F，过点F的直线交抛物线于A，B两点．
（1）若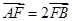
，求直线AB的斜率；
（2）设点M在线段AB上运动，原点O关于点M的对称点为C，求四边形OACB面积的最小值．
相关试题
的前
项和为
，且
，数列
中，
，点
在直线
上．（I）求数列
的通项
和
；
，求数列
的前n项和
，并求满足
的最大正整数
相关知识点
推荐套卷
（本小题满分12分）抛物线的焦点为F，过点F的直线交抛物线于A，B两点．
（1）若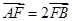，求直线AB的斜率；
（2）设点M在线段AB上运动，原点O关于点M的对称点为C，求四边形OACB面积的最小值．
粤公网安备 44130202000953号