(本小题满分12分)如图,已知底角为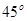 的等腰梯形
的等腰梯形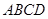 ,底边
,底边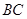 长为7
长为7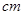 ,腰长为
,腰长为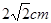 ,当一条垂直于底边
,当一条垂直于底边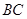
(垂足为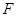 )的直线
)的直线 从左至右移动(与梯形
从左至右移动(与梯形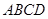 有公共点)时,直线
有公共点)时,直线 把梯形分成两部分,令
把梯形分成两部分,令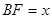 ,
,
(1)试写出直线 左边部分的面积
左边部分的面积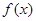 与
与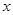 的函数.
的函数.
(2)已知 ,
,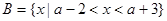 ,若
,若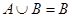 ,求
,求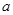 的取值范围.
的取值范围.
推荐套卷
(本小题满分12分)如图,已知底角为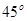 的等腰梯形
的等腰梯形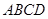 ,底边
,底边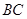 长为7
长为7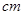 ,腰长为
,腰长为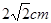 ,当一条垂直于底边
,当一条垂直于底边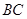
(垂足为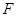 )的直线
)的直线 从左至右移动(与梯形
从左至右移动(与梯形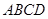 有公共点)时,直线
有公共点)时,直线 把梯形分成两部分,令
把梯形分成两部分,令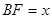 ,
,
(1)试写出直线 左边部分的面积
左边部分的面积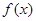 与
与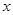 的函数.
的函数.
(2)已知 ,
,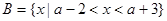 ,若
,若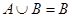 ,求
,求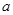 的取值范围.
的取值范围.