如图，在锐角△ABC中，AC是最短边；以AC中点O为圆心，
AC长为半径作⊙O，交BC于E，过O作OD∥BC交⊙O于D，连结AE、AD、DC．
（1）求证：D是弧ＡＥ的中点；
（2）求证：∠DAO =∠B +∠BAD；
（3）若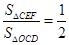
，且AC=4，求CF的长．
是函数
的切线，求
的值。
，求
时
的值。
，利用定义求
。
在
处的导数。
在
处的导数。推荐套卷
如图，在锐角△ABC中，AC是最短边；以AC中点O为圆心，AC长为半径作⊙O，交BC于E，过O作OD∥BC交⊙O于D，连结AE、AD、DC．
（1）求证：D是弧ＡＥ的中点；
（2）求证：∠DAO =∠B +∠BAD；
（3）若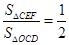，且AC=4，求CF的长．
粤公网安备 44130202000953号