﹣（π﹣3．14）0+2﹣1；相关试题
如图，已知AB∥CD，∠AEC=90°，那么∠A与∠C的度数和为多少度？为什么？
解：∠A与∠C的度数和为 _________ ．
理由：过点E作EF∥AB，
∵EF∥AB，
∴∠A+∠AEF=180°（ _________ ）．
∵AB∥CD（ _________ ），EF∥AB，
∴EF∥CD（ _________ ）
∴ _________ （两直线平行，同旁内角互补）
∴∠A+∠AEF+∠CEF+∠C= _________ °（等式的性质）
即∠A+∠AEC+∠C= _________ °
∵∠AEC=90°（已知）
∴∠A+∠C= _________ °（等式的性质）．
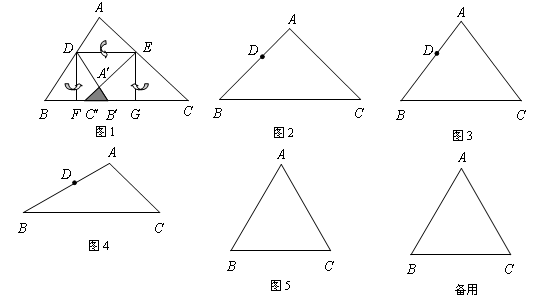
如图1，已知有一张三角形纸片ABC的一边AB=10，若D为AB边上的点，过点D作DE∥BC交AC于点E，分别过点D、E作DF⊥BC于F，EG⊥BC于G，把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠，点A、B、C分别落在A′、B′、C′处．若点A′、B′、C′在矩形DFGE内或者其边上，且互不重合，此时我们称△A′B′C′（即图中阴影部分）为“重叠三角形”．
实践探究：
（1）当AD=4时，
①若∠A=90°，AB=AC，请在图2中画出“重叠三角形”，S△A′B′C′= ；
②若AB=AC，BC=12，如图3，S△A′B′C′= ；
③若∠B=30°，∠C=45°，如图4，S△A′B′C′= .
（2）若△ABC为等边三角形（如图5），AD=m，且重叠三角形A′B′C′存在，试用含m的代数式表示重叠三角形A′B′C′ 的面积，并写出m的取值范围.
相关知识点
推荐套卷
粤公网安备 44130202000953号